Building a Balanced Universe
Hello everybody, my name is CCP Prism X and I am a Libra!
This summer we saw a welcome influx of players with the release of EVE Online: Odyssey. On occasions as such we usually celebrate our great success by pulling out the champagne and our $1000 Japanese pants, and having ourselves a great big pillow fight. However, this time around the influx of people was so dramatic that it worried us; Empire Space was burning. There were so many people in New Eden, doing so many things, that the actual CPU cores (reffered to as "nodes" hereafter) running the Empire Space systems were under extreme load. This was causing Time Dilation to affect the various, and disparate, portions of Empire Space. Time Dilation is all well and good when you‘re blobbing with your space-friends in Nullsec. But when you‘re just running a mission in some dead-end system, all alone in local, and suddenly everything starts going all bullet-time on you: you get frustrated.
Empire Space should really have such predictable load† that Time Dilation should never kick in there. If it happens, our Static Cluster Premapper should at least be able to avoid a reoccurence. That is because we track an estimated load fingerprint of all solar systems and assign systems to different nodes, based on said estimated load, during startup. As long as that estimate is correct-ish and the premapper is functioning as it should, things should run fairly smoothly. But the same systems were consistently starting up on nodes with too many other systems assigned to them. Things were not running very smoothly at all and we weren‘t quite sure why.
† Assuming that no social engineering takes place that diverts load to new, unexpected, places.
Example: Announcing an upcoming LP offer from a corporation that only has a single good agent in high-security space will result in a lot of new load in that agents system which the premapper cannot in any way anticipate.
Step 1: Identify the problem
Above I omitted a fairly important fact about this premapping of solar systems: systems within the same constellation want to stay on the same node. They want it so bad that they‘ll do so at the expense of balanced load distribution as they‘ll ignore the, load wise, most optimal node assignment if their preferred node is only 20% more loaded than the optimal one. This behavior causes a huge deviation between the load of different nodes whereas we‘d rather want the premapper to spread the load as evenly as possible over all the nodes available to it. Furthermore this behavior doesn‘t extend above the constellation level so effectively a node can run two whole constellations, but one is located in the Deep North and the other in the Deep South. So a fleet fight in the Deep South could enforce Time Dilation on the other constellation located in the Deep North. That‘s frustrating for the Deep North pilots!
Here is visualization of the clustering of systems to nodes in the old systems (Note, this is 3D data badly projected on a 2D plane so there‘s some skew). Systems of the same colour reside on the same nodes. You‘ll quickly notice that this is just a jumble of colours with little consistency. I‘ve drawn red circles around two clusters which all belong to the same node to show the distance between the two:

And to top it off this isn‘t even a good load distribution. The difference between node load is fairly staggering as you can see on the standard deviation values here:

But why were we clustering systems on the constellation level? Because a long time ago it was theorized that inter-node stargate jumps were more expensive than intra-node jumps. Presumably, that is due to the assumed overhead introduced by network latency. Now we know that this assumption is completely wrong and inter-node jumps are actually cheaper than their counterpart. A stargate jump requires the removal of the player from one system, and his introduction into another one. Splitting that work between two nodes spreads load better than doing it all on the same node.
Realizing this, we just decided to remove any such node affinity behavior from the premapping logic as a first step. Systems would just be assigned to nodes on the basis of the most loaded, unassigned, system being assigned to the least loaded node. That resulted in an amazingly well balanced cluster and the load problem was solved! But even though we‘d made a very balanced cluster the Time Dilation problem was now even more pronounced. Systems had just been semi-randomly assigned to nodes with no respect to locality and so we still had people in the Deep North affected by fleet fights in the Deep South. Revert the changes and put the thinking cap back on!
Step 2: Solve the problem
So we needed a way to split load between nodes whilst ensuring that all systems on a node belong to the same space-neighborhood. As a secondary concern we really did not want to increase the time premapping took, and we used the opportunity to completely nuke the old T-SQL code and recreate it as a Python module. That last decision, unsurprisingly, turned out to be the most important one as a procedural language with a large supporting ecosystem of available tools is much better geared to solve a procedural problem than a highly limited relational language.
With Python at our side we initially arrived at a fairly simple and approachable solution. As we‘re attempting to split up a cluster of stars with defined coordinates so that both halves are adjacent and equally weighted; why don‘t we just do that? If you split any coordinate system in half with a plane, both halves will be adjacent to each other and that solves the problem of proximity. That leaves us with a way of ensuring that both halves are close to equal in their load. As we keep track of each systems load this just becomes a matter of tweaking the split line iteratively in some sensible manner. That‘s not more complex than using the properties of Binary Search! We just have to move the split line a given distance towards the more heavy of the two halves, and then half the distance we‘ll move it on the next iteration. Theoretically we should bounce between both sides of the optimal split line for a while until we hit it. I say theoretically because we‘re not trying to find the optimal solution here, only a good enough solution in the least amount of time.
Here is a graph to help you visualize this process. Imagine the circle stands for the entire cluster of stars we want to split up. The stars themselves are not shown because they're not important, all that matters is that the split will not mix stars from the two distinct halves between them and that the load is as equal as possible.
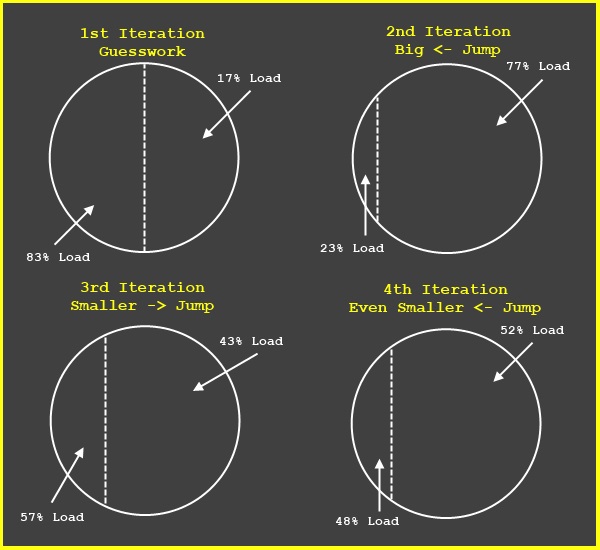
Once we’re done splitting the initial universe into two clusters, we’ll pick the heavier of those two and split it again. Then we’ll pick the heaviest of those three and split it again and repeat the process on the four resulting clusters of stars. We’ll repeat this until we have as many clusters as we have nodes at which point we commit the mapping to the database and continue on with startup.
To visualize this properly I’ve provided some visualization, using this method, run against the same dataset as the graph above. However, the first three steps are the split of Empire Space only due to the inner workings of the new method and only serve to describe the method better. The last picture is the final allocation of the entire universe (on the same data) and can thus be compared to the similar graph above.
First Empire Space split. Note the size difference of the two halves due to the fact that not all systems are equally loaded:

Seventh Empire Space split (that grey blob is two hues of gray):

End result of entire universe. Note how much more uniform the color distribution is:

Step 3: Actually Solve the Problem
That’s how we initially pushed out the new cluster premapper a few weeks before Rubicon was released. We did so understanding what the more Computer Sciency types out there might already have realized from the above; this results in a balanced load spread if, and only if, the number of nodes available for allocation are a whole power of two. Anything else will result in a fairly unbalanced load spread as we’re always splitting load into two halves, creating a sort of a Binary Tree. For a perfectly equal split we must have enough nodes to fill the leaf level of that imaginary tree or we’ll have nodes on level leaf-1 with double the amount of load on the nodes on the leaf level.
Here is a very simple picture displaying the whole power of two issue with 3 nodes as opposed to 2^2=4 nodes. Please keep in mind that this is a perfect world example. We do not actually expect all load splits to be perfectly equal.

This resulted in a too uneven of a split. The statistics below do look better for Nullsec but in Empire we’re still looking at a fairly large standard deviation between nodes. But at least the CPU Minimum isn’t zero here. Sadly the memory stats just got plain worse, but we’re really balancing primarily for CPU.

Obviously the optimal split here is 33% of the load allocated to each node but you can see how the nice and simple algorithm outlined above completely fails here. But since we know this works optimally if we divide the load by a number of nodes that is a whole level of two we just need to force that behavior! We could of course constrain ourselves to always have a whole power of two number of nodes for solar systems but that feels like a rather silly artificial constraint. Especially if you know that any number in base 10 (decimal number system) can be represented in base 2 (binary number system), then this just becomes a matter of rearranging the binary tree above into branches of whole number of two nodes and running the algorithm detailed above on those branches.
Using a bit more complex example than the three nodes above, we can visualize this in action as thus:

This is easy enough to achieve with minimal alterations to the code used in the initial solution. That solution already relies on a method of splitting coordinate systems in two equally loaded parts. Altering it to split it into two X/Y parts is no big deal.
Using this new approach on the exact same dataset as the examples above we end up with this pretty picture of a balanced universe within which space-friends shoot other space-friends in their respective faces:

And now the CPU standard deviation has dropped drastically! We're hoping to have this code out by tomorrow Wednesday, December 4th.

Step 4: Write a Dev Blog
Then do it again. This is the second version of this Dev Blog. I’m pretty sure nobody would have enjoyed reading the first one. Sadly I couldn’t reuse a lot of stuff from that first attempt, like I could with the code. It simply had too many mentions of water carriers, aqueducts and Beyonce Knowles. Probably wouldn’t have made a lot of sense to anybody!
So there you have it; our recipe for a Balanced Universe. Perhaps you can find some way of applying it to your own lives! I’m thinking those fancy colored dot charts could probably substitute for a Rorschach test. But in case you just read through my entire blog and do not feel like you’ve gained much from it I’d like to present you with this cool island song as a peace offering (Don’t browse at work kids!).
That’s it folks! If you’ve got some further questions I’ll be looking at the comment thread regularly.
